Research Interests
Quantum Measurements
- Quantum Bayesian Updates
Collecting partial information about a quantum system using a physical detector updates the quantum state according to a rule that generalizes Bayes' rule from classical probability theory. For superconducting qubits, the standard example is a quadrature measurement of an amplified microwave field that interacts with a qubit via a coupled resonator. Unlike textbook quantum measurements, the quantum state only partially "collapses" when partial information is collected. Moreover, these "partial collapses" may be probabilistically "uncollapsed" with later measurements.
- Weak Measurements
When almost no information is gathered by a detector making a measurement, the quantum state is almost entirely preserved. Nevertheless, taking a sufficiently large sample of data still permits the same average infomation to be extracted as a textbook measurement that fully collapses the state.
- Quantum Trajectories
Discretizing time into ideal infinitesimal pieces and applying both natural state evolution and measurement-induced Bayesian state updates at each time step yields a quantum trajectory. Generally these state trajectories show a competition between the natural evolution from the Schroedinger equation and the stochastic evolution from the measurement itself.
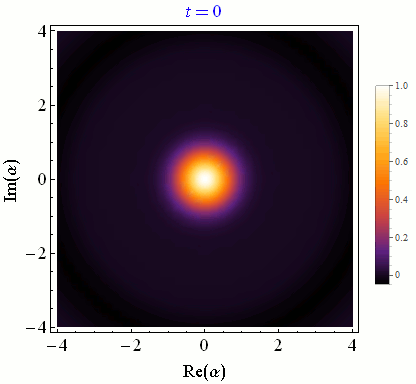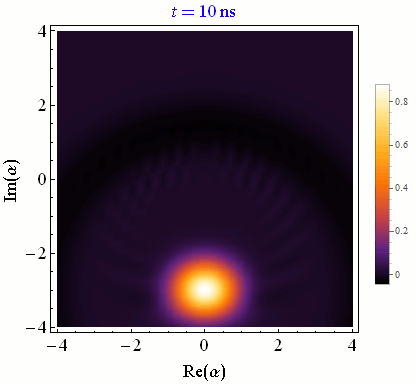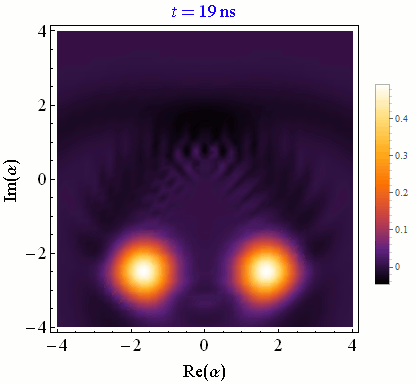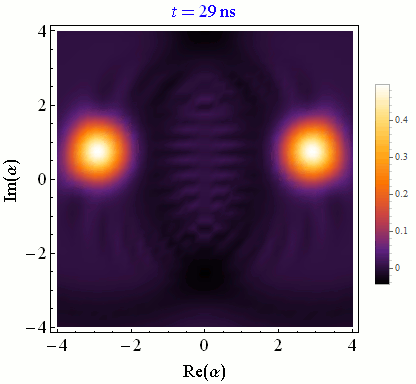
Catch-Disperse-Release
Wigner function evolution for resonator field mode states as they interact with a qubit either in the excited or the ground state [PRL 110, 2010501 (2013)]. When the lobes are well separated, a field quadrature measurement fully collapses the qubit indirectly, but when the lobes partially overlap that quadrature measurement only partially collapses the qubit.Quantum Computing with Superconducting Qubits
- Single-shot qubit readout
Fast and high-fidelity qubit readout is an essential part of quantum computing. In circuit QED we infer the state of a qubit by making a quadrature measurement on an interacting resonator field. It is important to quantify the sources of error (such as the Purcell effect) and develop robust readout strategies to combat these effects.
- Quantum feedback and control
One can continuously monitor partial information about a quantum system in order to control experimental parameters in real time for a variety of purposes, such as state purification and initializaiton, coherence stabilization, and error correction.
- Multi-qubit algorithms
The expected advantages of quantum computing are rooted in multi-qubit coherence and entanglement effects. Achieving precise control and characterization of multi-qubit protocols and implementations is a critically important focus of modern quantum computing research.
- Quantum state transfer
Transferring a quantum state from one qubit to another over a long distance while still preserving the coherence is a challenging task. We are investigating efficient transfer of a microwave field from one resonator to another using tunable couplers.
- Quantum Process Tomography
Determining how well one is implementing an algorithm in the lab is not a trivial matter. Modern methods under development use compressive sensing and adaptive estimation techniques to reduce the amount of data that one needs to collect, and reduce the computational resources required to reconstruct the estimates.
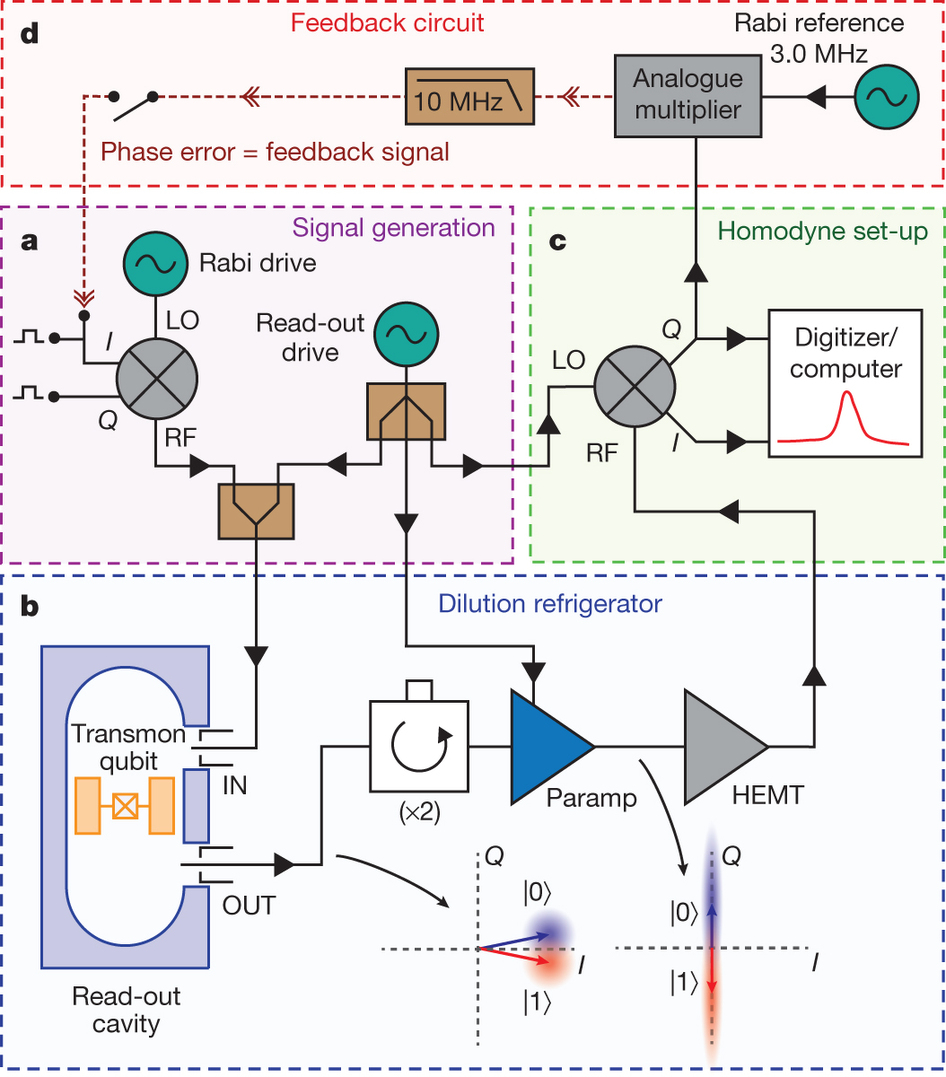
Rabi Oscillation Stabilization
Implementation of a feedback protocol that stabilizes the coherent qubit (Rabi) oscillations well beyond the natural decay rate of the hardware [courtesy of the Siddiqi group Nature 490, 77 (2012)].Research Funding
- Continuous quantum state tracking and error correction, ARO, 2015-2019
- Control of quantum open systems: theory and experiment, ARO MURI, 2011-2016
- Multi-qubit algorithms in Josephson phase qubits, ARO/IARPA, 2010-2015
- Algorithm demonstrations using Josephson qubits, ARO/IARPA, 2008-2010
- High-fidelity Josephson qubits, ARO/DTO, 2004-2009
- State purification and decoherence suppression by continuous measurement of a qubit, ARO, 2001-2004
- Background-charge-insensitive single-electron memories, SRC, 2001-2003

